6.5. Эжектор с фиксированной геометрией

Инструмент : эжектор с фиксированной геометрией; панель инструментов : создание оборудования для гидравлических схем

Эжектор с фиксированной геометрией служит для моделирования поведения эжектора с определенной геометрией при различных граничных условиях и составах входных потоков. Элемент данного типа имеет три базовых режима функционирования: режим определения максимального давления, режим определения давления по заданному статическому давлению на выходе, режим гидравлического элемента. В первых двух режимах элемент не включает в себя гидравлических переменных и уравнений, поэтому входные расходы не регулируются. Они рассчитываются и приводятся в диалоге элемента для справки. Расчет производится для заданного статического давления на выходе из эжектора. В первом режиме (максимального давления) выходной поток получает максимально возможное полное давление при данных условиях и расчетных расходах. При этом суммарный расход выходного потока равен сумме входных расходов, поэтому следует внимательно относиться к получаемым результатам и соотносить указанные и расчетные расходы. Во втором режиме выходной поток получает полное давление, которое соотвествует указанному статическому. Разница между двумя подходами проявляется только на критическом режиме эжектора, то есть при наличии скачка уплотнения в диффузоре. Первый режим исходит из условия отсутствия дополнительных потерь полного давления в скачке, второй – рассчитывает эти потери из условия заданного статического давления на выходе.

Режим использования эжектора в гидравлическом расчете включается в диалоге элемента. При этом активируется гидравлическая переменная – статическое давление на выходе, а также два гидравлических уравения – невязки расходов НД и ВД относительно расчетных. В простейшей схеме, в которой за эжектором стоит потребитель с заданным давлением, решение гидравлической задачи заключается в нахождении такого выходного статического давления эжектора, которому соотвествует фикисрованное давление в потребителе, и таких расходов НД и ВД, которые соответствуют режиму функционирования эжектора при заданных полных давлений НД и ВД и статическому выходному.

Эжектор задаеется через геометрические параметры (рис.6.5.12-8), это диаметры сечения ВД и НД, причем последний является также диаметром камеры смешения, выходной диаметр и диаметр диффузора. Последние два размера определяют угол раскрытия диффузора, влияющий на потери полного давления в нем. Длина камеры смешения в расчетах не используется. При выборе сверхзвукового эжектора дополнительно следует задать диаметр сопла ВД. Входные диаметры следует рассматривать не как размеры физического эжектора, а как параметры, определяющие площади входных сечений. Так, обозначив диаметр входа НД через \(d_2\), диаметр входа ВД через \(d_1\), соотвествующие площади сечений \(F_2\), \(F_1\) и площадь камеры смешения \(F_3\) определяются выражениями:

F_{1} = \frac{π {d_{1}}^{2}}{4}

F_{2} = \frac{π ({d_{2}}^{2} - {d_{1}}^{2})}{4}

F_{3} = \frac{π {d_{2}}^{2}}{4}

Рис.6.5.7 Сверхзвуковой эжектор

Рис.6.5.8 Звуковой эжектор

Расчет эжектора при заданных входных полных давлениях и выходном статическом давлении заключается в определении режима работы эжектора и соответствующих ему расходах входов НД и ВД. Предполагается, что обратные токи невозможны, то есть на входах стоят условные обратные клапана и при определенных условиях один или оба входа перекрываются. Всего рассматривается 11 возможных режимов. Режимы, в которых нет полного запирания, требуют хорошего согласования входных и выходного давлений, поэтому они трудно осуществимы, и, по определению, не являются рабочими для эжектора. Основным режимом является критический режим 6 (рис.6.5.9), именно для него далее будет приведена последовательность расчета. Расчет звукового эжектора отличается от сверхзвукового тем, что критическое (минимальное) \(F_{10}\) сечение совпадает с входом в камеру, при этом ряд режимов течения из полного списка теряют свою актуальность.

В таблице и далее под \(λ\) подразумевается относительная скорость, то есть отношение скорости потока к критической скорости потока при данной температуре.

Режимы течения в эжекторе

Номер режима

Описание

Расход ВД

Расход НД

Сверхзвук ВД

Сверхзвук НД

Запирание

перекрытие НД, сверхзвуковой по ВД

>0, \(λ_{10}=1\)

да

перекрытие НД, дозвук по ВД

>0, \(λ_{10}<1\)

нет

перекрытие ВД, дозвук по НД

>0, \(λ_{21}<1\)

нет

перекрытие ВД, сверхзвук по НД

>0, \(λ_{21}=1\)

да

перекрытие ВД и НД

основной закритический режим

>0, \(λ_{10}=1\)

>0, \(λ_{22}=1\)

да

дозвуковой режим

>0, \(λ_{10}<1\)

>0, \(P^{stat}_{11}=P^{stat}_{21}\)

нет

закритический с дозвуковым участком ВД

>0, \(λ_{10}=1\)

>0, \(λ_{21}<1\)

да

дозвук ВД, сверзвук НД

>0, \(λ_{10}<1\)

>0, \(λ_{21}=1\)

нет

да

нет

дозвук НД, сверзвук ВД

>0, \(λ_{10}=1\)

>0, \(λ_{22}<1\)

да

нет

сверхзвуковой

>0, \(λ_{10}=1\)

>0, \(λ_{21}=1\)

да

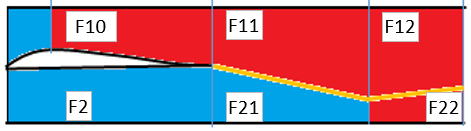Рис.6.5.9 Основной закритический режим

В основном режиме полагается \(λ_{10}=1\), что определяет расход ВД по формуле:

q = \frac{G \sqrt{2 \cdot C_{P} \cdot T}}{A (γ) \cdot P \cdot F}

A (γ) = γ \cdot {(\frac{2}{γ + 1})}^{\frac{1}{γ - 1}} \cdot \sqrt{\frac{γ + 1}{γ - 1}}

где \(G\) – массовый расход, \(C_P\) – удельная теплоемкость изобарного процесса, \(T\) – температура, \(F\) – площадь сечения, \(P\) – полное давление, индексы сечения опущены.

Газодинамическая функция \(q(λ,γ)\) в сечении 10 равна 1, а в общем случае определяется выражением:

q (λ, γ) = {(\frac{γ + 1}{2})}^{\frac{1}{γ - 1}} \cdot λ \cdot {(1 - \frac{γ - 1}{γ + 1} \cdot λ^{2})}^{\frac{1}{γ - 1}}

где \(γ=C_P/C_V\) – показатель адиабаты, 'C_V' – удельная теплоемкость изохорного процесса.

Значение \(λ_{11}\) определяется из условия

q (λ_{11}, γ_{1}) = \frac{F_{10}}{F_{11}}

где \(F_{10}\) – площадь сопла ВД, \(F_{11}\) – площадь ВД на входе в камеру смешения.

Значение \(λ_{21}\) подбирается итерационным процессом в пределах от 0 до 1 из уловия выполнения уравнения

z (λ_{11}) - z (λ_{12}) \cdot q (λ_{11}, γ_{1}) + Y \cdot q (λ_{21}, γ_{2}) \cdot (z (λ_{21}) - 2) = 0

где \(λ_{12}\) связано с \(λ_{21}\) уравнением

q (λ_{12}, γ_{1}) = \frac{a \cdot q (λ_{11}, γ_{1})}{1 + a \cdot q (λ_{21}, γ_{2})}

Здесь

z (λ) = λ + \frac{1}{λ}

a = \frac{F_{1}}{F_{2}}

Y = \frac{B (γ_{2}) \cdot A (γ_{2})}{B (γ_{1}) \cdot A (γ_{1}) \cdot a \cdot σ}

B (γ) = \sqrt{1 - \frac{1}{γ^{2}}}

σ = \frac{P_{1}}{P_{2}}

Расход НД определяется по той же формуле, что и для ВД, по полученному значению \(λ_{21}\) и площади \(F_{21}\). Далее определяется скорость на входе из камеры

n = \frac{G_{2}}{G_{1}}

θ = \frac{T_{2} C_{P 2}}{T_{1} C_{P 1}}

γ_{3} = \frac{γ_{1} γ_{2} (n C_{P 2} + C_{P 1})}{C_{P 1} γ_{2} + n C_{P 2} γ_{1}}

z (λ_{3}) = \frac{B (γ_{2}) \cdot n \cdot \sqrt{θ} \cdot z (λ_{2}) + B (γ_{1}) \cdot z (λ_{1})}{B (γ_{3})} \sqrt{\frac{n + 1}{n \cdot θ + 1}}

причем из двух решений для \(λ_{3}\) берется дозвуковое, то есть \(λ_{3}<1\)

Коэффициент повышения давления эжектора без учета диффузора и потерь в камере определяется по формуле

ϵ_{e j e c t} = \frac{P_{3}}{P_{2}} = \frac{(a + 1) \cdot σ \cdot q (λ_{1}, γ_{1}) \cdot A (γ_{1})}{q (λ_{3}, γ_{3}) \cdot A (γ_{3})} \sqrt{\frac{n θ + 1}{n + 1}}

Величина \(λ_3\) используется для расчета потерь в диффузоре, которые определяются по таблицам в зависимости от угла раскрытия диффузора [ 4 ] рис.6.5.10

M = \frac{λ_{3} \sqrt{2}}{\sqrt{(γ_{3} + 1) - (γ_{3} - 1) {λ_{3}}^{2}}}

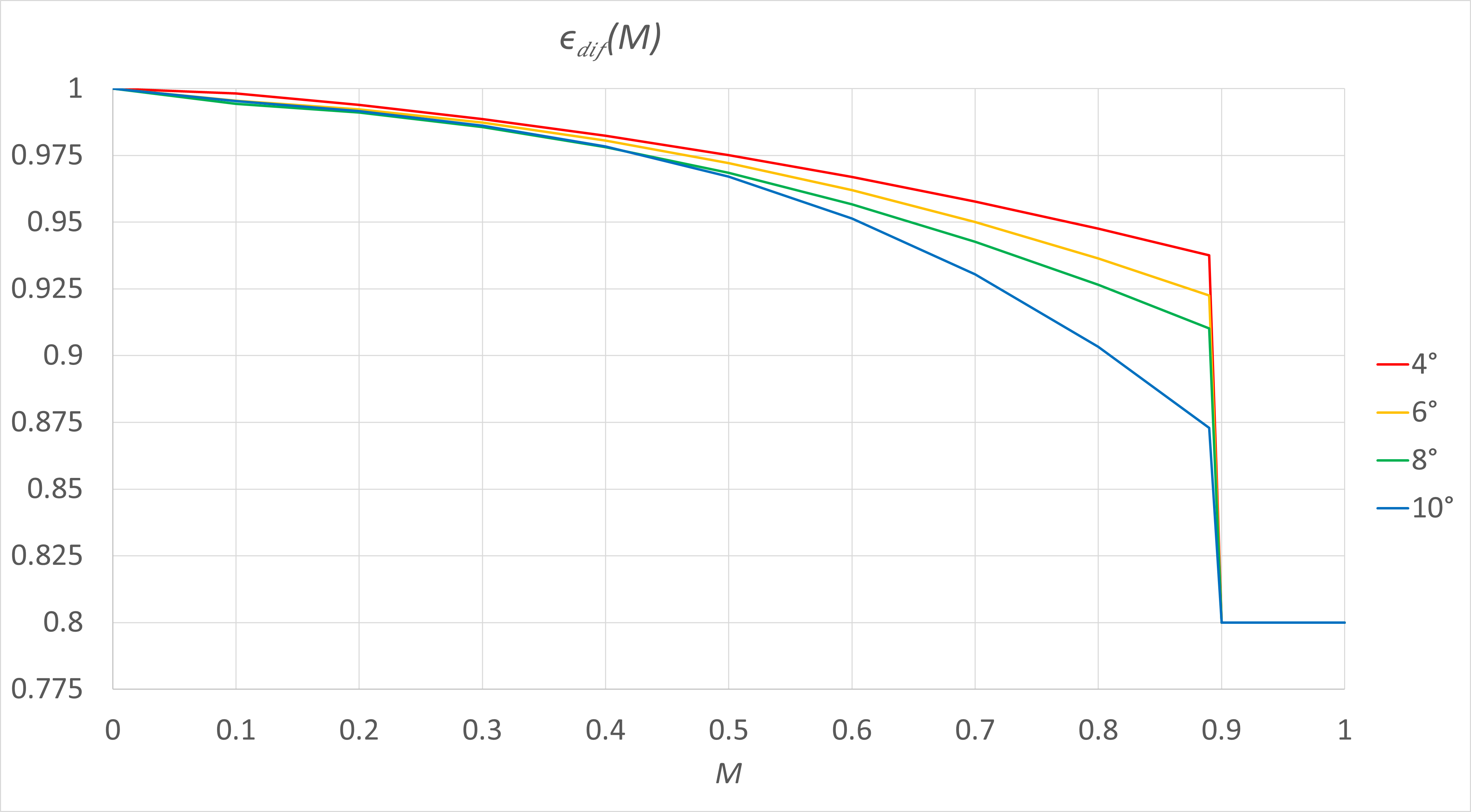Рис.6.5.10 Потери полного давления в диффузоре

Выходное давление \(P_{out}\) в итоге определяется через суммарный коэффициент повышения давления, который равен

ϵ = \frac{P_{o u t}}{P_{2}} = ϵ_{e j e c t} ϵ_{d i f} ϵ_{f r i c}

где \(ϵ_{fric}\) – коэффициент потерь на трение, задаваемый вручную. Если \(P_{out} > P_1/1.3\), то принимается \(P_{out} = P_1/1.3\). Статическое давление, соотвествующее расчитаннному полному выходному давлению, должно превышать заданное выходное статическое давление. В зависимости от режима расчета, это полное давление задается в выходном потоке, или же уменьшается до значения, которому соотвествует указанное пользователем или гидравлическим решателем выходное статическое давление.

Температура выходного потока определяется не по формулам расчета эжектора, а из условия сохранения энтальпии при приведении давления смеси к полученному выходному давлению.

Следует отметить, что формулы расчета эжектора явно или неявно опираются на модель идеального газа для ВД, НД и их смеси. В то же время, параметры потока, как теплоемкость, берутся из расчета смеси, причем допускается наличие жидкой фазы во входном потоке.

Диалог задания элемента типа "эжектор с фиксированной геометрией" приведен на рис.6.5.11-7.

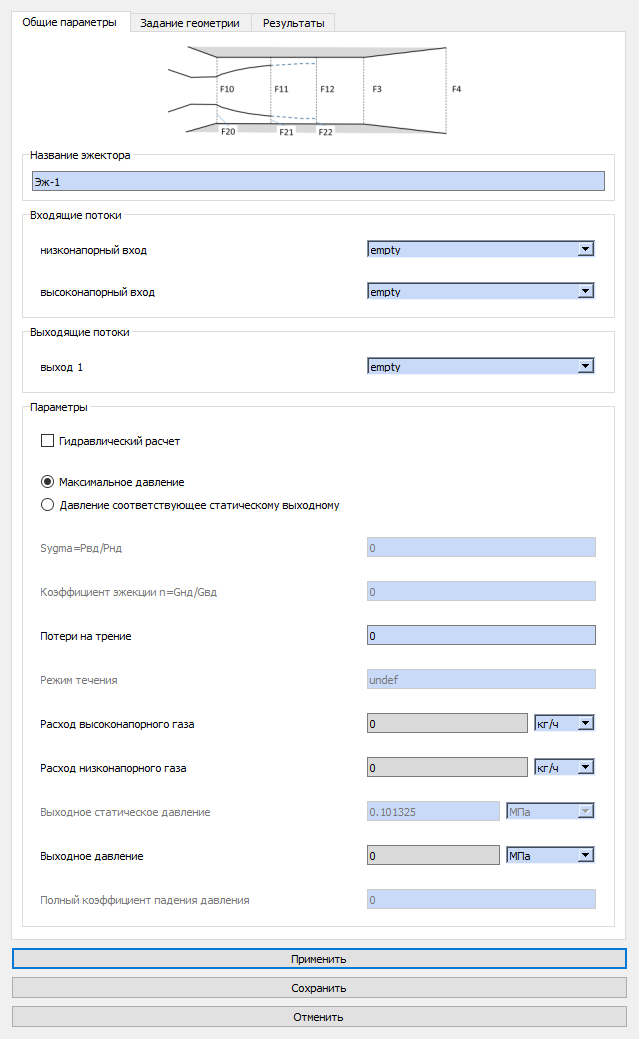Рис.6.5.11 Диалог задания эжектора

Рис.6.5.12 Диалог задания эжектора