8.9. Трубопровод гидравлический

Инструмент : труба гидр.; панель инструментов : создание оборудования для гидравлических схем

Элемент типа «трубопровод» моделирует течение однофазного или двухфазного флюида в трубе постоянного течения. При наличии водной фазы нефтяная и водная фаза объединяются в одну условную жидкую фазу. Помимо расчета падения давления, производится расчет выходной температуры с учетом теплообмена с внешней средой (воздух, вода или грунт) и наличии изоляции. Также элемент типа «трубопровод» используется для моделирования местных сопротивлений вроде отводов, тройников и т.д.

Один элемент соответствует участку трубопровода с постоянным уклоном, типоразмером трубы, параметрами изоляции и внешней среды. В случае существенных изменений этих характеристик по длине трубопровода создается последовательность элементов. Помимо этого, при расчете одного элемента он разбивается на заданное количество сегментов для повышения точности расчета протяженных трубопроводов.

Общая схема расчета одного элемента (сегмента) приведена на рис.ис.8.9.20. Схема содержит два вложенных итерационных процесса – внутренний по давлению, внешний по температуре. Падение давления зависит от вязкости флюида, которая в свою очередь, зависит от температуры и давления. Для начала итераций по внутреннему и внешнему циклам делаются оценки выходного давления и температуры соответственно. На их основе вычисляются средние температуры и давления сегмента. Средние температура и давление используются при расчете фазового равновесия и определения свойств флюида. Далее происходит расчет падения давления и получение новой оценки по выходному давлению. Если изменение величины выходного давления не превышает допустимой точности, то внутренний итерационный процесс считается сошедшимся и производится расчет теплообмена с определением нового значения выходной температуры. Иначе производится еще одна итерация по давлению. Аналогично, внешний итерационный процесс считается сошедшимся при условии, что изменение выходной температуры менее допустимой погрешности.

Выходные давление и температура сегмента являются начальными данными для следующего сегмента. В случае, если при текущем расходе выходное давление падает ниже 0 атм, элемент генерирует ошибку. Это служит сигналом для гидравлического решателя снизить расход в данной ветке.

Рис.8.9.20 Блок схема расчета элемента «трубопровод»

Расчет падения давления с учетом типа течения двухфазного флюида осуществляется по методике Беггза и Брилла [ 9 ].

Для однофазного флюида режим течения - турбулентный или ламинарный - определяется по числу Рейнольдса

N_{R e} = \frac{ρ v}{D μ}

где $ρ$ – плотность, $v$ – скорость, $D$ – внутренний диаметр, $μ$ – динамическая вязкость. При превышении 3250 течение считается турбулентным, иначе – ламинарным. Флюид, где присутствуют только жидкие фазы – углеводородная и водная, – также считается однофазным с точки зрения течения в трубопроводе.

Для ламинарного течения коэффициент трения равен

f = \frac{64}{N_{R e}}

для турбулентного определяется как решение уравнения Коулбрука-Уайта [ 10 ]

\frac{1}{\sqrt{f}} = - 2 {l o g}_{10} (\frac{ε}{3.7 D} + \frac{2.51}{N_{R e} \sqrt{f}})

где $ε$ – шероховатость стенки трубы.

Падение давления определяется по формуле

∆ P = \frac{f L ρ v^{2}}{2 D} + ρ g ∆ h

где $L$ – длина трубопровода, $g$ – ускорение свободного падения, $∆h$ – перепад высот между конечной и начальной точками трубопровода.

Для двухфазного флюида определяется число Фруда и параметры горизонтального течения

N_{F r} = \frac{{v_{M}}^{2}}{g D}

v_{M} = \frac{Q}{A}

λ_{L} = \frac{Q_{L}}{v_{M} A}

L_{1} = 316 {λ_{L}}^{0.302}

L_{2} = 0.009252 {λ_{L}}^{- 2.4684}

L_{3} = 0.1 {λ_{L}}^{- 1.4516}

L_{4} = 0.5 {λ_{L}}^{- 6.738}

где $v_M$ – скорость смеси, $Q$ – объемный расход, $Q_L$ – суммарный объемный расход нефтяной и водной фаз, $A$ – площадь внутреннего сечения трубы.

Тип течения определяется по следующим условиям

Раздельный (segregated)

$N_{F r} < L_{1}$ при $λ_{L} < 0.01$ ,

$N_{F r} < L_{2}$ при $λ_{L} \geq 0.01$ ,

Переходный (transition)

$L_{2} \leq N_{F r} \leq L_{3}$ при $λ_{L} \geq 0.01$ ,

Прерывистый (intermittent)

$L_{3} < N_{F r} \leq L_{1}$ при $0.01 \leq λ_{L} < 0.4$ ,

$L_{3} < N_{F r} \leq L_{4}$ при $λ_{L} \geq 0.4$ ,

Распределенный (distributed)

$N_{F r} \geq L_{1}$ при $λ_{L} < 0.4$ ,

$N_{F r} > L_{4}$ при $λ_{L} \geq 0.4$ .

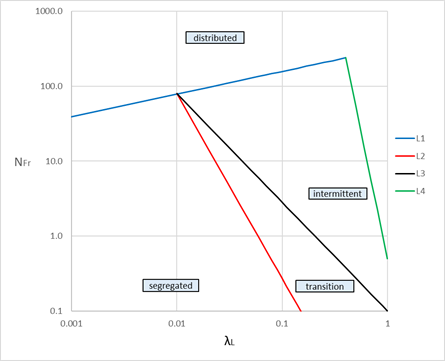
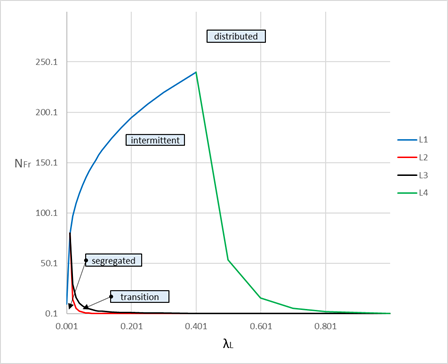
В координатах $λ_L-N_{Fr}$ разделение режимов показано на рис. 8.9.21 в логарифмической и нормальных шкалах.

Рис.8.9.21 Диаграмма режимов течения

Коэффициент объемного содержания жидкости для горизонтального трубопровода определяется как

H_{L} (0) = \frac{k_{1} {λ_{L}}^{k_{2}}}{{N_{F r}}^{k_{3}}}

коэффициенты $k_1$, $k_2$ и $k_3$ зависят от типа течения, само значение $H_L (0)$ не должно быть менее $λ_L$. При переходном режиме производится интерполяция

H_{L} (0) = A \cdot {H_{L} (0)}_{s e g r e g a t e d} + (1 - A) \cdot {H_{L} (0)}_{i n t e r m i t t e n t}

где $A = \frac{L_{3} - N_{F r}}{L_{3} - L_{2}}$ .

Коэффициенты для определения объемного содержания

Тип течения

$k_1$

$k_2$

$k_3$

Раздельный

0.98

0.4846

0.0868

Прерывистый

0.845

0.5351

0.0173

Распределенный

1.065

0.5824

0.0609

Коэффициент объемного содержания для наклонного трубопровода выражается через коэффициент для горизонтального случая по формуле

H_{L} (θ) = H_{L} (0) \cdot ψ

Здесь $θ$ – угол наклона трубопровода, положительный для восходящего трубопровода, для величины $ψ$ требуется провести следующие вычисления

ψ = 1 + α \cdot [\sin (1.8 θ) - 0.3333 \sin^{3} (1.8 θ)]

α = (1 - λ_{L}) \cdot l n (k_{4} {λ_{L}}^{k_{5}} {N_{L V}}^{k_{6}} {N_{F r}}^{k_{7}})

N_{L V} = v_{S L} {(\frac{ρ_{L}}{g σ})}^{0.25}

v_{S L} = \frac{Q_{w} + Q_{o}}{A}

ρ_{L} = ρ_{o} f_{o} + ρ_{w} f_{w}

f_{o} = \frac{Q_{o}}{Q_{o} + Q_{w}} = 1 - f_{w}

σ = σ_{o} f_{o} + σ_{w} f_{w}

где $σ_o$ и $σ_w$ – поверхностное натяжение, $Q_o$ и $Q_w$ – объемные расходы, $ρ_o$ и $ρ_w$ – плотности для нефтяной и водной жидкой фазы соответственно.

Коэффициенты для расчета поправки наклонного трубопровода

Тип течения

$k_4$

$k_5$

$k_6$

$k_7$

Раздельный

Восходящий

0.011

-3.768

3.539

-1.614

Прерывистый

Восходящий

2.96

0.305

-0.4473

0.0978

Распределенный

Восходящий

все

Нисходящий

4.7

-3.692

0.1244

-0.5056

Градиент давления по длине трубопровода состоит из трех частей

{[\frac{∆ P}{∆ L}]}_{t o t a l} = {[\frac{∆ P}{∆ L}]}_{e l e v} + {[\frac{∆ P}{∆ L}]}_{f r i c} + {[\frac{∆ P}{∆ L}]}_{a c c}

Здесь индекс total соответствует суммарному перепаду, fric – падению давления из-за трения, elev – падению или росту давления из-за перепада высот начальной и конечной точек трубопровода, acc – падение давления вследствие ускорения, что существенно только для флюидов с высоким газосодержанием. Учитывая зависимость последнего члена уравнения от суммарного перепада,

{[\frac{∆ P}{∆ L}]}_{a c c} = \frac{ρ_{S} {v_{M} v}_{S G}}{P} {[\frac{∆ P}{∆ L}]}_{t o t a l}

ρ_{S} = ρ_{g} + H_{L} (θ) (ρ_{L} - ρ_{g})

где $v_{SG}=Q_g/A$, $Q_g$ – объемный расход газовой фазы, $P$ – начальное давление, $ρ_g$ – плотность газовой фазы, формула суммарного падения давления принимает вид

{[\frac{∆ P}{∆ L}]}_{t o t a l} = \frac{{[\frac{∆ P}{∆ L}]}_{e l e v} + {[\frac{∆ P}{∆ L}]}_{f r i c}}{1 - \frac{ρ_{S} {v_{M} v}_{S G}}{P}}

Падение давления из-за перепада высот

{[\frac{∆ P}{∆ L}]}_{e l e v} = g ρ_{S} \sin θ

Падение давления вследствие трения

{[\frac{∆ P}{∆ L}]}_{f r i c} = \frac{f_{t p} ρ_{n} {v_{M}}^{2}}{2 D}

где $ρ_n=λ_L ρ_L+(1-λ_L ) ρ_g$, а для определения коэффициента трения $f_{tp}$ выполняются следующие вычисления

Y = \frac{λ_{L}}{{H_{L} (θ)}^{2}}

$β = \frac{l n (Y)}{- 0.0523 + 3.182 l n (Y) - 0.8725 {l n (Y)}^{2} + 0.01853 {l n (Y)}^{4}}$ , $Y > 1.2$ ,

$β = l n (2.2 Y - 1.2)$ , $1 \leq Y \leq 1.2$ ,

μ_{L} = μ_{o} f_{o} + μ_{w} f_{w}

N_{R e, n} = \frac{(ρ_{L} λ_{L} + ρ_{g} (1 - λ_{L})) v_{M} D}{μ_{L} λ_{L} + μ_{g} (1 - λ_{L})}

\frac{1}{\sqrt{f_{n}}} = - 2 {l o g}_{10} (\frac{ε}{3.7 D} + \frac{2.51}{N_{R e, n} \sqrt{f_{n}}})

f_{t p} = f_{n} \cdot e x p (β)

где $μ_g$, $μ_o$ $μ_w$ - динамические вязкости газовой, нефтяной и водной фаз. Для определения $f_n$ решается нелинейное уравнение.

Теплообмен с окружающей средой характеризуется теплотой, переданной от флюида в окружающую среду – $∆Q$. Эта величина может быть задана пользователем напрямую, с нулевым значением для отключения теплообмена. Иначе она считается по формуле

∆ Q = \frac{T^{o u t} - T^{i n}}{l n \frac{T^{e x t} - T^{i n}}{T^{e x t} - T^{o u t}}} \cdot F \cdot U

где $F$ – площадь поверхности теплообмена по внутреннему диаметру трубы, $U$ – суммарный коэффициент теплопередачи, $T^{ext}$ – температура среды.

Суммарный коэффициент теплопередачи включает в себя коэффициенты теплопередачи между флюидом и стенкой трубы $h_{flow}$, стенки трубы $h_{wall}$, изоляции при ее наличии $h_{isol}$, между трубой или изоляцией и внешней средой $h_{env}$:

\frac{1}{U} = \frac{1}{h_{f l o w}} + \frac{1}{h_{w a l l}} + \frac{D}{h_{i s o l} D_{e x t}} + \frac{D}{h_{e n v} D_{i s o l}}

Здесь $D$ – внутренний диаметр трубы, $D_{ext}$ – внешний диаметр трубы, $D_{isol}$ – внешний диаметр изоляции.

Коэффициент теплопередачи между флюидом и трубой считается по корреляции Петухова

h_{f l o w} = \frac{λ}{D} \cdot \frac{f}{8} \cdot \frac{N_{R e} N_{P r}}{1.07 + 12.7 \sqrt{f / 8} \cdot ({N_{R e}}^{2 / 3} - 1)}

где $N_{Re}$ – число Рейнольдса для флюида, $N_{Pr}=(C_p μ)/λ$ – число Прандтля для флюида, $λ$ – коэффициент теплопроводности флюида, $C_p$ – теплоемкость флюида, $μ$ – динамическая вязкость флюида, коэффициент трения, расчет которого описан выше.

Для коэффициентов теплопередачи стенки трубы и изоляции формулы имеют вид

h_{w a l l} = \frac{λ_{w a l l}}{l n (\frac{D_{e x t}}{D}) D}

h_{i s o l} = \frac{λ_{i s o l}}{l n (\frac{D_{i s o l}}{D_{e x t}}) D_{e x t}}

где $λ_{wall}$ и $λ_{isol}$ – коэффициенты теплопроводности стенки трубы и изоляции соответственно.

Коэффициент теплопередачи между изоляцией и внешней средой зависит от типа внешней среды. Для воздуха или воды данный коэффициент определяется по корреляции Холмана

h_{e n v} = \frac{λ_{e n v}}{D_{i s o l}} \cdot \frac{{N_{R e}}^{0.6} {N_{P r}}^{0.38}}{4}

где $λ_{env}$ – теплоемкость внешний среды, $N_{Re}$ – число Рейнольдса для внешней среды, зависящее от скорости обтекания, $N_{Pr}$ – число Прандтля для внешней среды. Необходимые для определения чисел Рейнольдса и Прандтля параметры внешней среды берутся из встроенных табличных данных для воздуха и воды. Для подземного трубопровода формула для расчета коэффициента теплопередачи рассчитывается по формуле Форхгеймера [ 11 ]

h_{e n v} = \frac{2 \cdot λ_{s o i l}}{D_{i s o l} \cdot l n (\frac{2 Z + \sqrt{4 Z^{2} - {D_{i s o l}}^{2}}}{D_{i s o l}})}

где $λ_{soil}$ – коэффициент теплопроводности грунта, $Z$ – глубина заложения трубопровода.

Элемент типа трубопровод используется также для моделирования местных сопротивлений вроде отводов, тройников, обратных клапанов и т. п. В данном случае никаких гипотез о типе течения флюида не выдвигается, падение давления определяется по формуле

∆ P = ς {(\frac{0.0101}{D^{0.2232}})}^{m} \frac{ρ v^{2}}{2}

где $ς$ – коэффициент местного сопротивления, $m$ – показатель степени, равный 0 или 1. Коэффициенты $ς$ и $m$ для некоторых встроенных типов сопротивлений приведены в таблице ниже.

Коэффициенты местного сопротивления

Тип элемента

$ς$

$m$

Отвод 90 градусов

Отвод 45 градусов

Отвод 180 градусов

Угловой клапан

Двустворчатый клапан

Шаровой кран

Задвижка (откр)

Шаровой вентиль

340

Подъемно-обратный клапан

600

Тарельчатый клапан

420

Обратный клапан (поворотный)

100

Обратный клапан (шаровой)

400

Тройник (разветвленный заглушенный)

Тройник (колено)

Внезапное сужение канала 2:1

Внезапное сужение канала 4:1

9.6

Внезапное сужение канала 4:3

Вход в отверстие с острыми краями

0.25

Вход

0.78

Внезапное расширение канала 2:1

Внезапное расширение канала 4:1

225

Внезапное расширение канала 4:3

0.6

Колено 90гр

Сужение канала 2:1

5.67

Сужение канала 4:3

0.65

Выход из канала

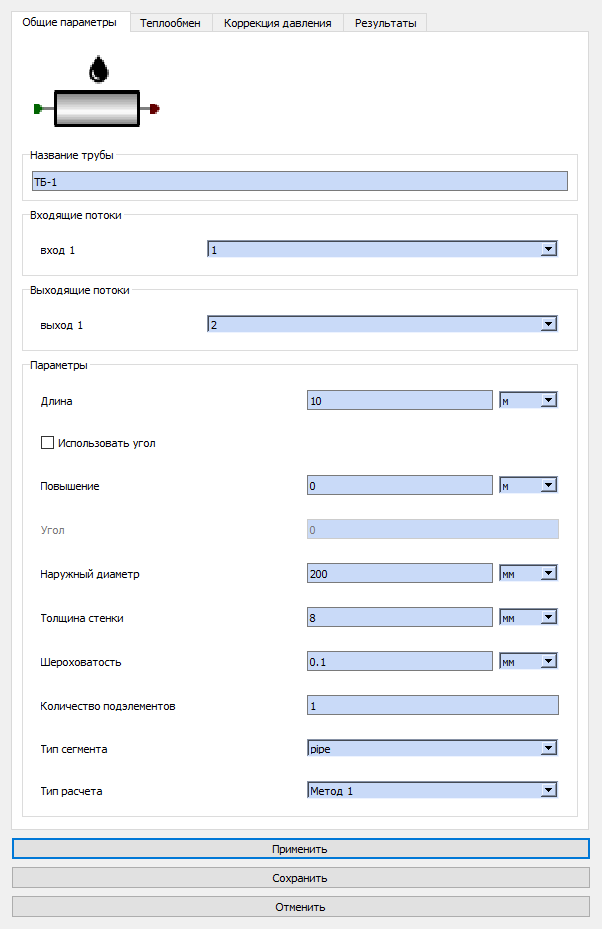
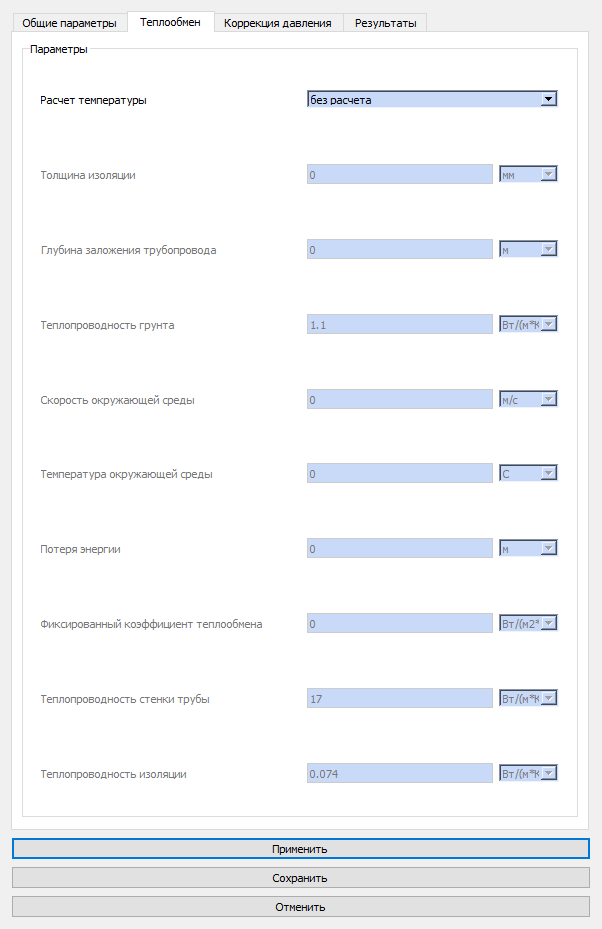
Диалог задания трубопровода предаставлен на рис.8.9.22. На вкладке коррекция давления (рис.8.9.23) пользователь может задать корректирующий множитель по давлению, который, как правило, определяется в процессе настройки расчетной схемы по имеющимся измерениям. На последней вкладке приводится информация расчета для всех подэлементов.

Рис.8.9.22 Диалог задания трубопровода

Рис.8.9.23 Диалог задания трубопровода