6.3. Теплообменник кожухотрубчатый

Инструмент : теплообменник кожухотрубчатый; панель инструментов : создание оборудования

Расчет теплообменника кожухотрубчатого [ 2 ] осуществляется с помощью теплообменника универсального, коэффициенты КТП в 6.2.1 рассчитываются по геометрическим параметрам аппарата. Диалог задания теплообменника представлен на рис.6.3.3 и рис.6.3.4.

Площадь теплообмена определяется по внутренней поверхности труб

$$F_{in} = \pi \cdot d_{in} \cdot L \cdot n \cdot k $$

где $d_{in}$ – внутренний диаметр труб, $L$ – длина камеры, $n$ – количество труб в одном проходе, $k$ – количество проходов, для U-образного теплообменника $k=2$.

Формула для коэффициента теплопередачи 6.2.1 содержит коэффициенты теплообмена трубного пространства $K_{in}$ и межтрубного пространства $K_{out}$, термического сопротивления труб с учетом отложений $R_{wall}$:

$$K=\frac{N}{\frac{1}{K_{in}} +R_{wall}+\frac{F_{in}}{K_{out} \cdot F_{out}}}$$

$$F_{out} = \pi \cdot (d_{in}+2\delta)\cdot L \cdot n \cdot k$$

здесь $\delta$ – толщина стенок труб, $N$ – количество подключенных последовательно аппаратов. Для расчета сопротивления труб используется формула

$$ R_{wall} = \frac{1}{s_{in}}+ \frac{1}{s_{out}} +\frac{d_{in} \cdot ln(\frac{d_{in}+2\delta}{d_{in}})}{2\lambda _{wall}} $$

где $λ_{wall}$ – коэффициент теплопроводности материала труб, $s_{in}$ и $s_{out}$ - тепловая проводимость загрязнений на внутренней и наружной поверхностях труб соответственно.

$$K_{in}=\frac{Nu_1 \cdot \lambda _1 }{d_{in}}$$

$$Nu_1=0.023\cdot Re_1^{0.8} \cdot Pr_1^{0.4}$$

$$Re_1= \frac{\rho _1 \cdot d_{in} \cdot v_1 }{ \mu_1} $$

$$Pr_1= \frac { \mu _1 \cdot C_{P1} }{\lambda_1} $$

$$S_1 = \frac{\pi \cdot d_{in}^2 \cdot n}{4}$$

$$v_1 = \frac{G_1}{ \rho_1 \cdot S_1 }$$

где $\lambda_1$ , $\rho _1$ и $\mu_1$ – средние значения, определяемые как полусумма свойств входящего и исходящего потока (для текущей оценки температуры исходящего потока).

Для потока межтрубного пространства

$$K_{out} = Nu_2 \cdot \frac{\lambda _2 }{d_{in}+2\delta}$$

$$Nu_2=0.24 \cdot Re_2^{0.6} \cdot Pr_2^{0.34}$$

$$Re_2 = \frac{\rho _2 \cdot (d_{in}+2\delta) \cdot v_2}{\mu_2}$$

$$Pr_2 = \frac{\mu _2 \cdot C_{P2}}{\lambda _2}$$

где $\lambda_2$ , $\rho _2$ и $\mu_2$ – средние значения, определяемые аналогично значениям для первого потока.

$$v_2 =\frac{G_2 \cdot 4}{\rho_2 \cdot S_2 }$$

$$S_2 = \frac{L\cdot x}{P+2} \cdot \frac{D_{ch}+d_{in}+2\delta}{{x+d_{in}+2\delta}}$$

где $x$ – шаг труб, $P$ – количество перегородок, $D_{ch}$ – внутренний диаметр камеры. Эта формула приблизительно оценивает поперечный просвет между трубами в центре трубы. Здесь в корреляции для числа Нуссельта указаны коэффициенты для турбулентного режима.

Параметры для универсального теплообменника приведены в диалоге оборудования и определяются по формулам:

$F = N \cdot F_{in}$ – площадь теплообмена,

$\delta _{eq} = R_{wall} \cdot \lambda _{wall}$ – эквивалентная толщина стенки труб,

$\lambda _{wall}$ – коэффициент теплопроводности материала труб,

$n_1 = 0.8$, $m_1=0.4$, $n_2=0.6$, $m_2=0.34$ – показатели степени,

$b_1=0.023 \frac{d_{in}^{0.8-1}}{S_1^{0.8}}$ , $b_2=0.24 \frac{(d_{in}+2\delta)^{0.6-1}}{S_2^{0.6}}$.

В разделе "Результаты" диалога приведены рассчитанные значения подведенной или отведенной теплоты в единицу времени для каждого потока и величина среднего логарифмического температурного напора.

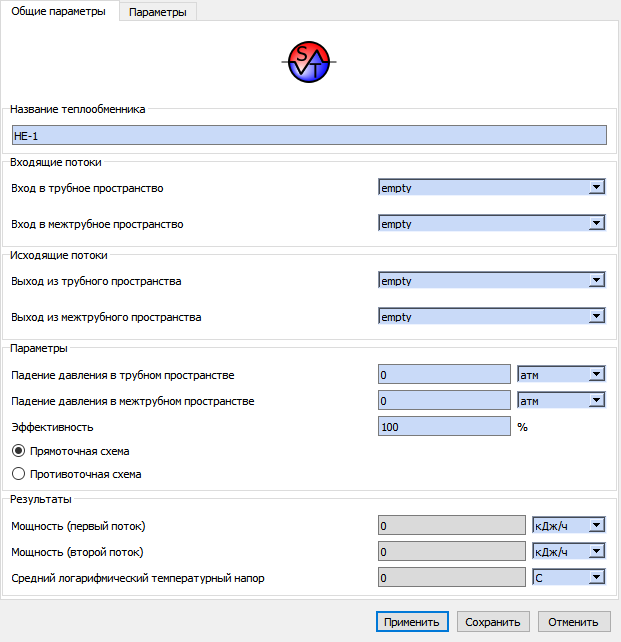Рис.6.3.3 Диалог задания теплообменника кожухотрубчатого

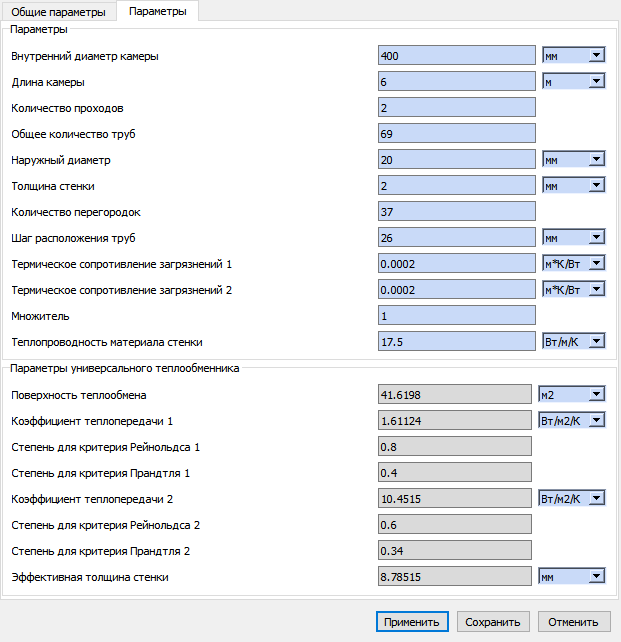Рис.6.3.4 Геометрические параметры теплообменника кожухотрубчатого